Diagramme de Bode
(d'après CCINP)On considère un filtre dont le diagramme de Bode (en amplitude et en phase) est donné ci-dessous :
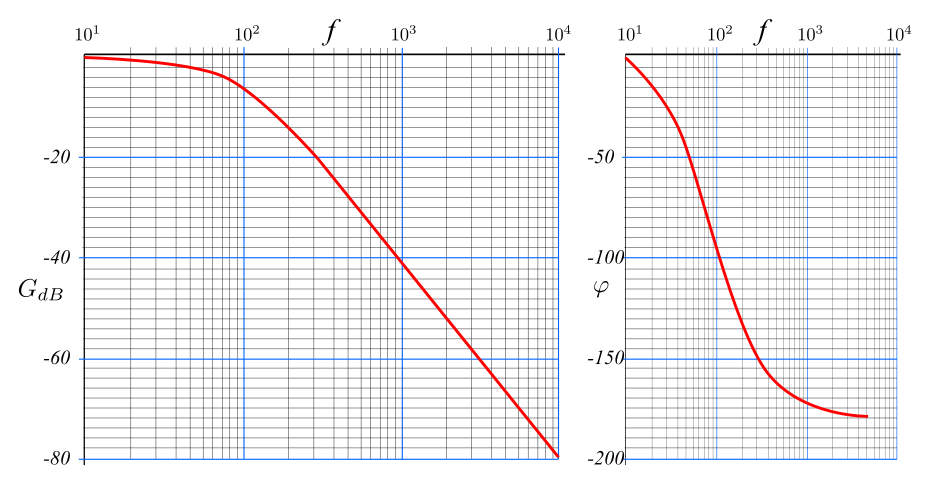
- Quelle est la nature du filtre ?
- Quel est son ordre ?
- En entrée du filtre, \(e(t) = E\cos(2\pi ft)\) avec \(E=5 \si V\). Donner la tension de sortie pour \(f = 10 \si{Hz}\), \(f = 100 \si{Hz}\), \(f = 10^4 \si{Hz}\).
Savoir-faire :
- Détermination de la nature et de l'ordre d'un fitre à partir de son diagramme de Bode.
- Exploitation de la définition de la fonction de transfert pour déduire les caractéristiques (amplitude et phase/déphasage) de la tension de sortie connaissant la tension d'entrée et le diagramme de Bode.
- Nature du filtre
- Tension de sortie
Ordre du filtre